12.3 从一棵FP树中挖掘频繁项集

实际上，到现在为止大部分比较困难的工作已经处理完了。接下来写的代码不会再像12.2节那样多了。有了FP树之后，就可以抽取频繁项集了。这里的思路与Apriori算法大致类似，首先从单元素项集合开始，然后在此基础上逐步构建更大的集合。当然这里将利用FP树来做实现上述过程，不再需要原始数据集了。

从FP树中抽取频繁项集的三个基本步骤如下：

1. 从FP树中获得条件模式基；
2. 利用条件模式基，构建一个条件FP树；
3. 迭代重复步骤1和步骤2，直到树包含一个元素项为止。

接下来重点关注第1步，即寻找条件模式基的过程。之后，为每一个条件模式基创建对应的条件FP树。最后需要构造少许代码来封装上述两个函数，并从FP树中获得频繁项集。

12.3.1　抽取条件模式基

首先从上一节发现的已经保存在头指针表中的单个频繁元素项开始。对于每一个元素项，获得其对应的条件模式基（conditional pattern base）。条件模式基是以所查找元素项为结尾的路径集合。每一条路径其实都是一条前缀路径（prefix path）。简而言之，一条前缀路径是介于所查找元素项与树根节点之间的所有内容。

回到图12-2，符号r的前缀路径是{x,s}、{z,x,y}和{z}。每一条前缀路径都与一个计数值关联。该计数值等于起始元素项的计数值，该计数值给了每条路径上r的数目。表12-3列出了上例当中每一个频繁项的所有前缀路径。

表12-3　每个频繁项的前缀路径

前缀路径将被用于构建条件FP树，但是现在暂时先不需要考虑这件事。为了获得这些前缀路径，可以对树进行穷举式搜索，直到获得想要的频繁项为止，或者使用一个更有效的方法来加速搜索过程。可以利用先前创建的头指针表来得到一种更有效的方法。头指针表包含相同类型元素链表的起始指针。一旦到达了每一个元素项，就可以上溯这棵树直到根节点为止。

下面的程序清单给出了前缀路径发现的代码，将其添加到文件fpGrowth.py中。

程序清单12-4　发现以给定元素项结尾的所有路径的函数

def ascendTree(leafNode, prefixPath):
    #❶ 迭代上溯整棵树 
    if leafNode.parent != None:
        prefixPath.append(leafNode.name)
        ascendTree(leafNode.parent, prefixPath)

def findPrefixPath(basePat, treeNode):
    condPats = {}
    while treeNode != None:
        prefixPath = 
        ascendTree(treeNode, prefixPath)
        if len(prefixPath) > 1:
            condPats[frozenset(prefixPath[1:])] = treeNode.count
        treeNode = treeNode.nodeLink
    return condPats
  

上述程序中的代码用于为给定元素项生成一个条件模式基，这通过访问树中所有包含给定元素项的节点来完成。当创建树的时候，使用头指针表来指向该类型的第一个元素项，该元素项也会链接到其后续元素项。函数findPrefixPath遍历链表直到到达结尾。每遇到一个元素项都会调用ascendTree来上溯FP树，并收集所有遇到的元素项的名称❶。该列表返回之后添加到条件模式基字典condPats中。

使用之前构建的树来看一下实际的运行效果：

>>> reload(fpGrowth)
<module \'fpGrowth\' from \'fpGrowth.py\'>
>>> fpGrowth.findPrefixPath(\'x\', myHeaderTab[\'x\'][1])
{frozenset([\'z\']): 3}
>>> fpGrowth.findPrefixPath(\'z\', myHeaderTab[\'z\'][1])
{}
>>> fpGrowth.findPrefixPath(\'r\', myHeaderTab[\'r\'][1])
{frozenset([\'x\', \'s\']): 1, frozenset([\'z\']): 1,frozenset([\'y\', \'x\', \'z\']): 1} 
  

读者可以检查一下这些值与表12-3中的结果是否一致。有了条件模式基之后，就可以创建条件FP树。

12.3.2　创建条件FP树

对于每一个频繁项，都要创建一棵条件FP树。我们会为z、x以及其他频繁项构建条件树。可以使用刚才发现的条件模式基作为输入数据，并通过相同的建树代码来构建这些树。然后，我们会递归地发现频繁项、发现条件模式基，以及发现另外的条件树。举个例子来说，假定为频繁项t创建一个条件FP树，然后对{t,y}、{t,x}重复该过程，…。元素项t的条件FP树的构建过程如图12-4所示。

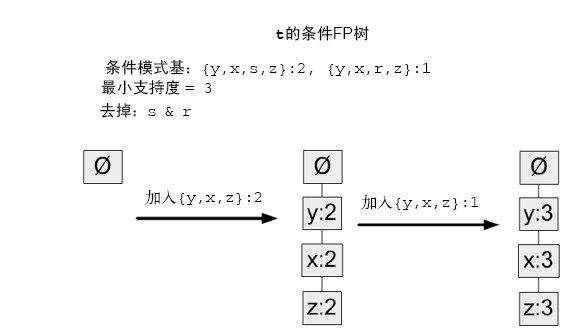
图12-4　t的条件FP树的创建过程。最初树以空集作为根节点。接下来，原始的集合{y,x,s,z}中的集合{y,x,z}被添加进来。因为不满足最小支持度要求，字符s并没有加入进来。类似地，{y,x,z}也从原始集合{y,x,r,z}中添加进来

在图12-4中，注意到元素项s以及r是条件模式基的一部分，但是它们并不属于条件FP树。原因是什么？如果讨论s以及r的话，它们难道不是频繁项吗？实际上单独来看它们都是频繁项，但是在t的条件树中，它们却不是频繁的，也就是说，{t,r}及{t,s}是不频繁的。

接下来，对集合{t,z}、{t,x}以及{t,y}来挖掘对应的条件树。这会产生更复杂的频繁项集。该过程重复进行，直到条件树中没有元素为止，然后就可以停止了。实现代码相对比较直观，使用一些递归加上之前写的代码就可以完成。打开fpGrowth.py，将下面程序中的代码添加进去。

程序清单12-5　递归查找频繁项集的mineTree函数

def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
    #❶ 从头指针表的底端开始
    bigL = [v[0] for v in sorted(headerTable.items,key=lambda p: p[1])]
    for basePat in bigL:
        newFreqSet = preFix.copy
        newFreqSet.add(basePat)
        freqItemList.append(newFreqSet)
        condPattBases = findPrefixPath(basePat, headerTable[basePat][1])
        #❷ 从条件模式基来构建条件FP树
        myCondTree, myHead = createTree(condPattBases,minSup)
        #❸ 挖掘条件FP树
        if myHead != None:
            mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)   
  

创建条件树、前缀路径以及条件基的过程听起来比较复杂，但是代码起来相对简单。程序首先对头指针表中的元素项按照其出现频率进行排序。（记住这里的默认顺序是按照从小到大。）❶然后，将每一个频繁项添加到频繁项集列表freqItemList中。接下来，递归调用程序清单12-4中的findPrefixPath函数来创建条件基。该条件基被当成一个新数据集输送给createTree函数。❷这里为函数createTree添加了足够的灵活性，以确保它可以被重用于构建条件树。最后，如果树中有元素项的话，递归调用mineTree函数 ❸。

下面将整个程序合并到一块看看代码的实际运行效果。将程序清单12-5中的代码添加到文件fpGrowth.py中并保存，然后在Python提示符下输入：

>>> reload(fpGrowth)
<module \'fpGrowth\' from \'fpGrowth.py\'>
  

下面建立一个空列表来存储所有的频繁项集：

>>> freqItems =   
  

接下来运行mineTree，显示出所有的条件树：

>>> fpGrowth.mineTree(myFPtree, myHeaderTab, 3, set(), freqItems)
conditional tree for: set([\'y\'])
    Null Set   1
      x   3
        z   3
conditional tree for: set([\'y\', \'z\'])
    Null Set   1
      x   3
conditional tree for: set([\'s\'])
    Null Set   1
      x   3
conditional tree for: set([\'t\'])
    Null Set   1
      y    3
        x   3
          z   3
conditional tree for: set([\'x\', \'t\'])
    Null Set   1
      y   3
conditional tree for: set([\'z\', \'t\'])
    Null Set   1
      y   3
        x   3
conditional tree for: set([\'x\', \'z\', \'t\'])
    Null Set   1
      y   3
conditional tree for: set([\'x\'])
    Null Set   1
      z   3
  

为了获得类似于前面代码的输出结果，我在函数mineTree中添加了两行：

print \'conditional tree for: \',newFreqSet
myCondTree.disp(1)
  

这两行被添加到程序中语句if myHead != None:和mineTree函数调用之间。

下面检查一下返回的项集是否与条件树匹配：

>>> freqItems
[set([\'y\']), set([\'y\', \'z\']), set([\'y\', \'x\', \'z\']), set([\'y\', \'x\']),set([\'s\']), set([\'x\', \'s\']), set([\'t\']), set([\'y\', \'t\']), set([\'x\',\'t\']), set([\'y\', \'x\', \'t\']), set([\'z\', \'t\']), set([\'y\', \'z\', \'t\']),set([\'x\', \'z\', \'t\']), set([\'y\', \'x\', \'z\', \'t\']), set([\'r\']), set([\'x\']),set([\'x\', \'z\']), set([\'z\'])]
  

正如我们所期望的那样，返回项集与条件FP树相匹配。到现在为主，完整的FP-growth算法已经可以运行，接下来在一个真实的例子上看一下运行效果。我们将看到是否能从微博网站Twitter中获得一些常用词。