为克服k均值算法收敛于局部最小值的问题,有人提出了另一个称为二分k均值(bisecting K-means)的算法。该算法首先将所有点作为一个簇,然后将该簇一分为二。之后选择其中一个簇继续进行划分,选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值。上述基于SSE的划分过程不断重复,直到得到用户指定的簇数目为止。
二分k均值算法的伪代码形式如下:
将所有点看成一个簇
当簇数目小于k时
对于每一个簇
计算总误差
在给定的簇上面进行K均值聚类(K=2)
计算将该簇一分为二之后的总误差
选择使得误差最小的那个簇进行划分操作
另一种做法是选择SSE最大的簇进行划分,直到簇数目达到用户指定的数目为止。这个做法听起来并不难实现。下面就来看一下该算法的实际效果。打开kMeans.py文件然后加入下面程序清单中的代码。
程序清单10-3 二分K均值聚类算法
def biKmeans(dataSet, k, distMeas=distEclud):
m = shape(dataSet)[0]
clusterAssment = mat(zeros((m,2)))
#❶(以下两行)创建一个初始簇
centroid0 = mean(dataSet, axis=0).tolist[0]
centList =[centroid0]
for j in range(m):
clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2
while (len(centList) < k):
lowestSSE = inf
for i in range(len(centList)):
#❷(以下两行)尝试划分每一簇
ptsInCurrCluster =dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]
centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2 , distMeas)
sseSplit = sum(splitClustAss[:,1])
sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])
print \"sseSplit, and notSplit: \",sseSplit,sseNotSplit
if (sseSplit + sseNotSplit) < lowestSSE:
bestCentToSplit = i
bestNewCents = centroidMat
bestClustAss = splitClustAss.copy
lowestSSE = sseSplit + sseNotSplit
#❸(以下两行)更新簇的分配结果
bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] =len(centList)
bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] =bestCentToSplit
print \'the bestCentToSplit is: \',bestCentToSplit
print \'the len of bestClustAss is: \', len(bestClustAss)
centList[bestCentToSplit] = bestNewCents[0,:]
centList.append(bestNewCents[1,:])
clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss
return mat(centList), clusterAssment
上述程序中的函数与程序清单10-2中函数kMeans的参数相同。在给定数据集、所期望的簇数目和距离计算方法的条件下,函数返回聚类结果。同kMeans一样,用户可以改变所使用的距离计算方法。
该函数首先创建一个矩阵来存储数据集中每个点的簇分配结果及平方误差,然后计算整个数据集的质心,并使用一个列表来保留所有的质心❶。得到上述质心之后,可以遍历数据集中所有点来计算每个点到质心的误差值。这些误差值将会在后面用到。
接下来程序进入while循环,该循环会不停对簇进行划分,直到得到想要的簇数目为止。可以通过考察簇列表中的值来获得当前簇的数目。然后遍历所有的簇来决定最佳的簇进行划分。为此需要比较划分前后的SSE。一开始将最小SSE置设为无穷大,然后遍历簇列表centList中的每一个簇。对每个簇,将该簇中的所有点看成一个小的数据集ptsInCurrCluster。将ptsInCurrCluster输入到函数kMeans中进行处理(K = 2)。k均值算法会生成两个质心(簇),同时给出每个簇的误差值❷。这些误差与剩余数据集的误差之和作为本次划分的误差。如果该划分的SSE值最小,则本次划分被保存。一旦决定了要划分的簇,接下来就要实际执行划分操作。划分操作很容易,只需要将要划分的簇中所有点的簇分配结果进行修改即可。当使用kMeans函数并且指定簇数为2时,会得到两个编号分别为0和1的结果簇。需要将这些簇编号修改为划分簇及新加簇的编号,该过程可以通过两个数组过滤器来完成❸。最后,新的簇分配结果被更新,新的质心会被添加到centList中。
当while循环结束时,同kMeans函数一样,函数返回质心列表与簇分配结果。
下面看一下实际运行效果。将程序清单10-3中的代码添加到文件kMeans.py并保存,然后在Python提示符下输入:
>>> reload(kMeans)
<module \'kMeans\' from \'kMeans.py\'>
可以在最早的数据集上运行上述过程,也可以通过如下命令来导入图10-2中那个“较难”的数据集:
>>> datMat3=mat(kMeans.loadDataSet(\'testSet2.txt\'))
要运行函数biKmeans,输入如下命令:
>>> centList,myNewAssments=kMeans.biKmeans(datMat3,3) sseSplit, and notSplit: 491.233299302 0.0 the bestCentToSplit is: 0 the len of bestClustAss is: 60 sseSplit, and notSplit: 75.5010709203 35.9286648164 sseSplit, and notSplit: 21.40716341 455.304634485 the bestCentToSplit is: 0 the len of bestClustAss is: 40
现在看看质心结果:
>>> centList
[matrix([[-3.05126255, 3.2361123 ]]), matrix([[-0.28226155, -2.4449763 ]]),
matrix([[ 3.1084241, 3.0396009]])]
上述函数可以运行多次,聚类会收敛到全局最小值,而原始的kMeans函数偶尔会陷入局部最小值。图10-3给出了数据集及运行biKmeans后的的质心的示意图。
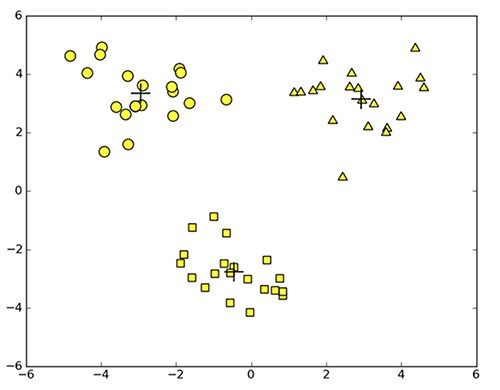
图10-3 运行二分K均值算法后的簇分配示意图,该算法总是产生较好的聚类结果
前面已经运行了二分K均值算法,下面将该算法应用于一些真实的数据集上。下一节将利用地图上的地理位置坐标进行聚类。
